Skip to contents

paretoPlot

Source: R/3.3_Factorial_designs_Functions.R
paretoPlot.Rd

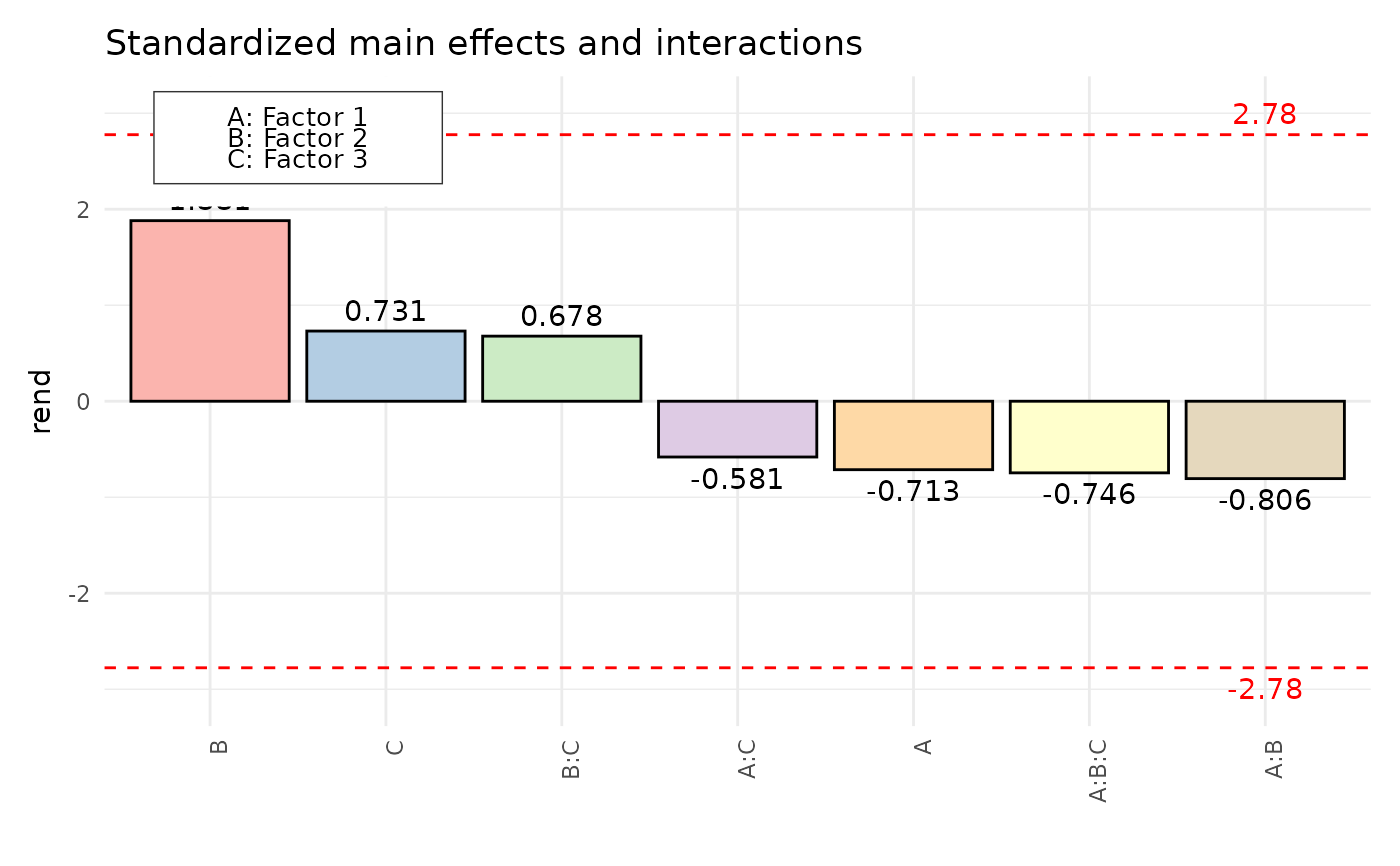
Display standardized effects and interactions of a facDesign.c object in a pareto plot.

Usage

paretoPlot(
  dfac,
  abs = TRUE,
  decreasing = TRUE,
  alpha = 0.05,
  response = NULL,
  ylim,
  xlab,
  ylab,
  main,
  p.col,
  legend_left = TRUE
)

Arguments

dfac

An object of class facDesign.

abs

Logical. If TRUE, absolute effects and interactions are displayed. Default is TRUE.

decreasing

Logical. If TRUE, effects and interactions are sorted decreasing. Default is TRUE.

alpha

The significance level used to calculate the critical value

response

Response variable. If the response data frame of fdo consists of more then one responses, this variable can be used to choose just one column of the response data frame. response needs to be an object of class character with length of `1`. It needs to be the same character as the name of the response in the response data frame that should be plotted. By default response is set to NULL.

ylim

Numeric vector of length 2: limits for the y-axis. If missing, the limits are set automatically.

xlab

Character string: label for the x-axis.

ylab

Character string: label for the y-axis.

main

Character string: title of the plot.

p.col

Character string specifying the color palette to use for the plot. Must be one of the following values from the RColorBrewer package:

  • `Set1`

  • `Set2`

  • `Set3`

  • `Pastel1`

  • `Pastel2`

  • `Paired`

  • `Dark2`

  • `Accent`

legend_left

Logical value indicating whether to place the legend on the left side of the plot. Default is TRUE.

Value

The function paretoPlot returns an invisible list containing:

effects

a list of effects for each response in the facDesign.c object

plot

The generated PP plot.

Details

paretoPlot displays a pareto plot of effects and interactions for an object of class facDesign (i.e. 2^k full or 2^k-p fractional factorial design). For a given significance level alpha, a critical value is calculated and added to the plot. Standardization is achieved by dividing estimates with their standard error. For unreplicated fractional factorial designs a Lenth Plot is generated.

See also

fracDesign, facDesign

Examples

# Create the facDesign object
dfac <- facDesign(k = 3, centerCube = 4)
dfac$names(c('Factor 1', 'Factor 2', 'Factor 3'))

# Assign performance to the factorial design
rend <- c(simProc(120,140,1), simProc(80,140,1), simProc(120,140,2),
          simProc(120,120,1), simProc(90,130,1.5), simProc(90,130,1.5),
          simProc(80,120,2), simProc(90,130,1.5), simProc(90,130,1.5),
          simProc(120,120,2), simProc(80,140,2), simProc(80,120,1))
dfac$.response(rend)

paretoPlot(dfac)

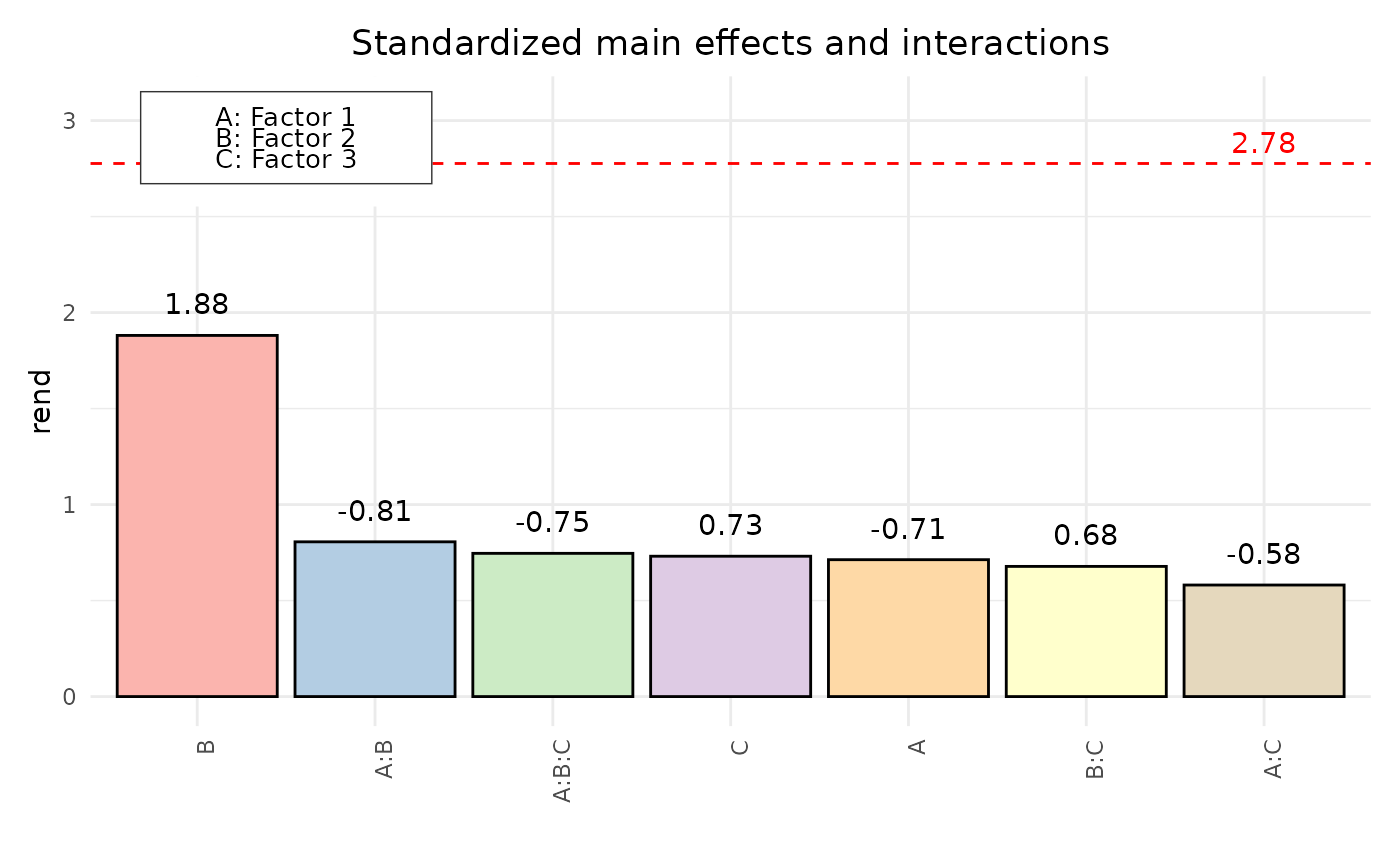paretoPlot(dfac, decreasing = TRUE, abs = FALSE, p.col = "Pastel1")