Skip to contents

gageRR: Gage R&R - Gage Repeatability and Reproducibility

Source: R/2.3_gageRR_Functions.R
gageRR.Rd

Performs a Gage R&R analysis for an object of class gageRR.c.

Usage

gageRR(
  gdo,
  method = "crossed",
  sigma = 6,
  alpha = 0.25,
  tolerance = NULL,
  dig = 3,
  print = TRUE
)

Arguments

gdo

Needs to be an object of class gageRR.c.

method

Character string specifying the Gage R&R method. `crossed` which is the typical design for performing a Measurement Systems Analysis using Gage Repeatability and Reproducibility or `nested` which is used for destructive testing (i.e. the same part cannot be measured twice). Operators measure each a different sample of parts under the premise that the parts of each batch are alike. By default method is set to `crossed`.

sigma

Numeric value giving the number of sigmas. For sigma=6 this relates to 99.73 percent representing the full spread of a normal distribution function (i.e. pnorm(3) - pnorm(-3)). Another popular setting sigma=5.15 relates to 99 percent (i.e. pnorm(2.575) - pnorm(-2.575)). By default sigma is set to `6`.

alpha

Alpha value for discarding the interaction Operator:Part and fitting a non-interaction model. By default alpha is set to `0.25`.

tolerance

Mumeric value giving the tolerance for the measured parts. This is required to calculate the Process to Tolerance Ratio. By default tolerance is set to NULL.

dig

numeric value giving the number of significant digits for format. By default dig is set to `3`.

print

Print the summary of the perform of the Gage.

Value

The function gageRR returns an object of class gageRR.c and shows typical Gage Repeatability and Reproducibility Output including Process to Tolerance Ratios and the number of distinctive categories (i.e. ndc) the measurement system is able to discriminate with the tested setting.

See also

gageRR.c, gageRRDesign, gageLin, cg.

Examples

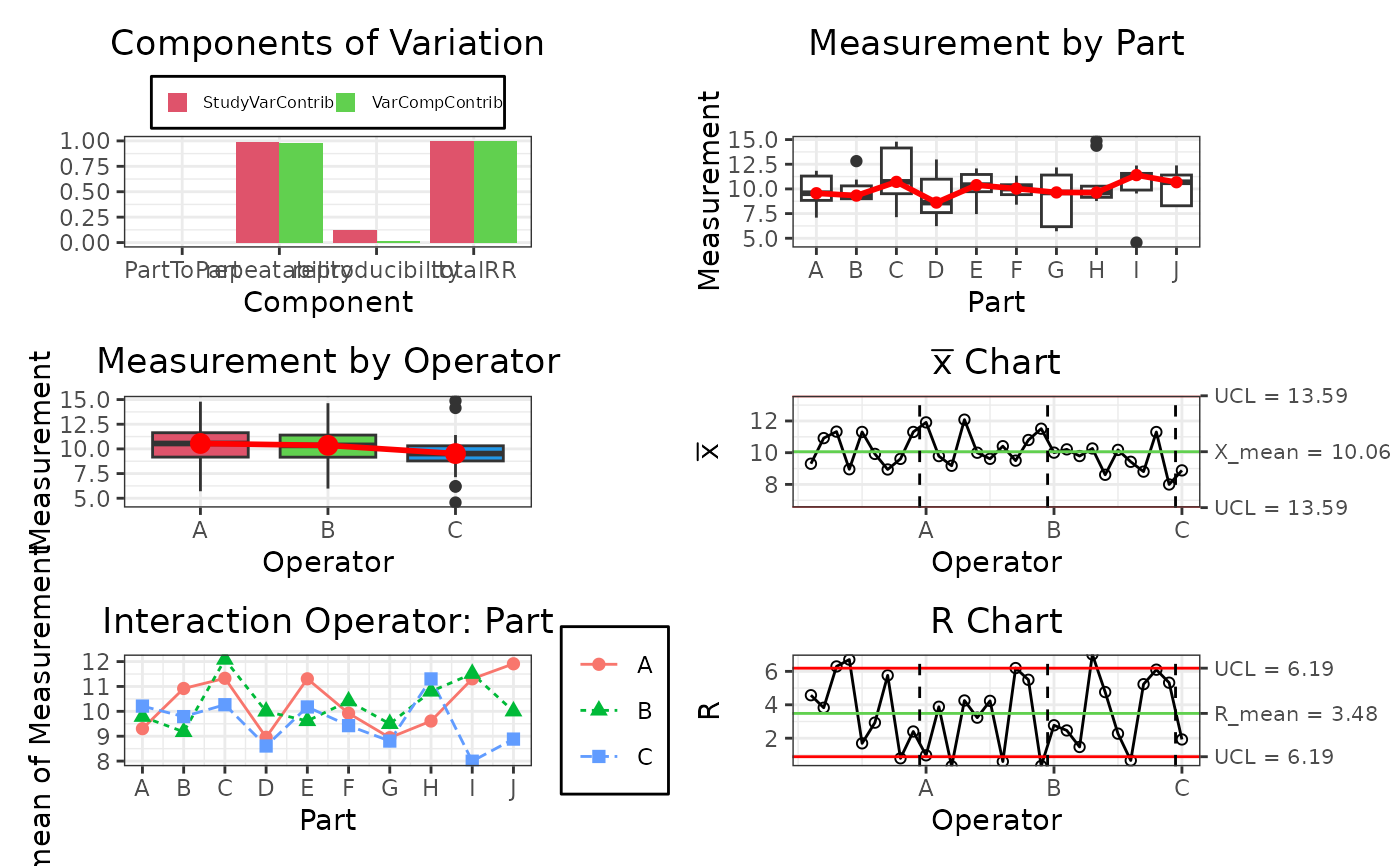
# Create de gageRR Design
design <- gageRRDesign(Operators = 3, Parts = 10, Measurements = 3,
                       method = "crossed", sigma = 6, randomize = TRUE)
design$response(rnorm(nrow(design$X), mean = 10, sd = 2))

# Results of de Design
result <- gageRR(gdo = design, method = "crossed", sigma = 6, alpha = 0.25)
#> 
#> AnOVa Table -  crossed Design
#>               Df Sum Sq Mean Sq F value Pr(>F)
#> Operator       2  12.01   6.007   1.360  0.264
#> Part           9  32.73   3.637   0.824  0.597
#> Operator:Part 18  50.75   2.819   0.638  0.854
#> Residuals     60 264.96   4.416               
#> 
#> ----------
#> AnOVa Table Without Interaction -  crossed Design
#>             Df Sum Sq Mean Sq F value Pr(>F)
#> Operator     2  12.01   6.007   1.484  0.233
#> Part         9  32.73   3.637   0.899  0.531
#> Residuals   78 315.71   4.048               
#> 
#> ----------
#> 
#> Gage R&R
#>                  VarComp VarCompContrib Stdev StudyVar StudyVarContrib
#> totalRR           4.1128         1.0000 2.028    12.17           1.000
#>  repeatability    4.0475         0.9841 2.012    12.07           0.992
#>  reproducibility  0.0653         0.0159 0.256     1.53           0.126
#>    Operator       0.0653         0.0159 0.256     1.53           0.126
#>    Operator:Part  0.0000         0.0000 0.000     0.00           0.000
#> Part to Part      0.0000         0.0000 0.000     0.00           0.000
#> totalVar          4.1128         1.0000 2.028    12.17           1.000
#> 
#> ---
#>  * Contrib equals Contribution in %
#>  **Number of Distinct Categories (truncated signal-to-noise-ratio) = 1 
#> 
class(result)
#> [1] "gageRR.c" "R6"      
result$plot()